For decades chess authors, players and columnists have tried to foresee the moment when the chess computer finally beats the top player once and for all. John Smith is playing Kasparov a thousand times and is going to lose a thousand times. But little John would have a statistical chance, even if it is very unlikely, of winning, if only they would just play an infinite number of games. It’s then only a matter of time, of probability and coincidence. Everyone who knows the rules would eventually score the one crucial point in a match of infinite duration, even a two year old child. Clearly, the probability is extremely low but the reality does not therefore change. If you are Kramnik you would need two games on average to get a point from Kasparov, if you are Michael Adams you may need 3 games to reach the target, a Julian Hodgson may need 5 and Harriet Hunt 10 and so on…and John Smith with his 100 BCF may need a million games on average but eventually he will be a winner. To make this experimental idea reasonable and logically correct one has to see the named player not as a real person but as an abstract entity which never changes through getting older, feelings, moods, tiredness, sentiments, history and so on, in short: as a model or an eternal player.

With the chess playing computer this hypothetical idea becomes a reality. The programmed computer is an eternal player. It holds its strength for all time, provided that it is without a selflearning option and it is based on unchangeable hard- and software parameters. But in reality those hard- and software parameters are in a rapid development, they now calculate an astronomical amount of moves and will multiply that amount still further on – for the moment there is no end to be seen. Compared with the human brain, it looks like a very unfair competition; our calculation capacity is biologically restricted. So it seems to be quite logical to think, that the computer must overcome us soon. Already in 1957 experts forecasted this event within the next ten years, but men still are able to play against computers successfully and success does not automatically have to mean a win - simply a balanced game, i.e. it’s still not like John Smith v Garry Kasparov. And it will never be so! This is the thesis of the present article.

Isn’t it rather amazing that devilish machines calculating millions and millions of moves in only one second still can’t win more games against humans (i.e. the best of them). Even if they calculate billions of moves, they never reach that crucial point. And this is not because they are lacking intuition or strategic understanding, as people still thoughtlessly say; it is because of a sheer logic phenomenon. All those impressive numbers, provided as argument, contain a false conclusion: they suggest, as a sequence of numbers, infinity. Yet chess is not an infinite game! Its possibilities are enormous but not endless. Chess is a numerically finite game.

On the other hand: professional chess, because of its new scientific approach, because of the steadily growing scientific community and, last but not least, because of the cooperation with computers and databases itself, has made a huge qualitative step forward. And every step forward in a finite frame means a step towards the absolute possibilities of the game and we can presume that at the highest level, chess is now coming very near that frame or border. One must not misunderstand: this is about the qualitative not the quantitative state of the game. There is no sense in pointing out the still existing huge number of possible, reasonable and still unplayed moves and positions. To get the picture, imagine a container. The more the container is filled the less is still available in it: in a 10 % filled container there is a relatively huge scope, but in a 90% filled container there is a relatively little scope. In the case of chess we can assume that the container of possibilities will never be completely full and, even though the frame may be slightly elastic, we’re heading towards that point. The still missing definitive success of the always becoming faster computer is therefore a sign that the game is dangerously near the inherent border zone. Even exponential improvements cause in that area relatively small progress. In other words, we have to deal with a border line phenomenon (Grenzphänomen) as in the diagram.

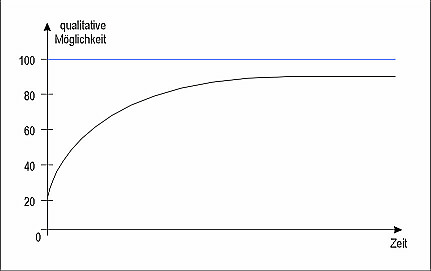
If the above is correct, than we have to face certain consequences.
Capablancas statement of the "drawing death” (Remistod) gains new meaning. The top level players neutralize each other, not because they are highly trained and knowledgeable – this only holds true for the opening preparation which nowadays often extends into the endgame – but because they have reached that ideal zone. They can only arrive at a draw. Therefore often it is not the case that the better player is winning but that the weaker player is losing. With that there is the obvious disappearance of "evergreen”, "immortal” and charismatic games. True genius moves are becoming rare; instead we find more genius errors and their refutation. Because of the limits we can’t say who really is the best anymore (we could do that during Morphy’s time and still during Fischer’s); to do so we have to invent secondary parameters such as, for instance, time (Who is the best with certain conditions – Kasparov is the best in classic play but would he be the best in 1 minute Blitz game or in correspondence chess?). If two mountain climbers are within just 100 metres of the peak of Mount Everest, it’s nearly impossible to say who is the better one, who would be able to climb the greatest height.

Now the talk of the end of chess acquires a new meaning but with essential limitations:

1. The majority of chess players don’t have to worry; although even they are getting closer to the peak, they’re still miles away, they’re still in an earlier state of chess evolution.

2. This only holds true in the rather narrow frame of the actual rules. Fischer-Random, Janus Chess and other variants open up new countless possibilities as new rules would do (for example to count the stalemate as a win for the active side).

3. We can’t rule out a new revolution in chess understanding - the appearance of a new Steinitz. This may sound absurd but initially a revolutionary idea always sounds absurd.